Quantitative apptitude for any competitive exams LCM,HCF,NUMBERS,DIVISABILITY,

                                                     QUANTITATIVE APPTITUDE


TYPES OF NUMBERS

1. Integers : All numbers whose fractional part is 0 (zero) like -3, -2, 1, 0, 10, 100 are integers.
2. Natural Numbers : Counting numbers like 1, 2, 3, 4, 5, 6 … Basically, all integers greater than 0 are natural numbers.
3. Whole Numbers : All natural numbers and 0 (zero) are whole numbers.
4. Prime Numbers : All numbers having only two distinct factors, the number itself and 1, are called prime numbers. Some prime numbers are 2, 3, 53, 67 and 191.
5. Composite Numbers : All numbers greater than 1 which are NOT prime are composite numbers. Some composite numbers are 4, 60, 91 and 100.

IMPORTANT POINTS ON PRIME NUMBERS

• 1 is neither prime, nor composite.
• 2 is the only even prime number.
• There are 25 prime numbers less than 100. They are : 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
• To check if a number ‘p’ is prime, find a number ‘n’ such that ‘n’ is the smallest natural number which satisfies n2 >= p. Now, check if ‘p’ is divisible by any of the prime numbers less than or equal to ‘n’. If ‘p’ is NOT divisible by any such prime numbers, ‘p’ is a prime number. Otherwise, p is not a prime number.
• Co-primes : Two numbers ‘a’ and ‘b’ are called co-prime if their highest common factor (HCF) is 1.

DIVISIBILITY TESTS

• Divisibility By 2 : A number is divisible by 2 if the last digit is any of 0, 2, 4, 6, 8.
• Divisibility By 3 : A number is divisible by 3 if the sum of its digits is divisible by 3. For example, 12321 is divisible by 3 because 1 + 2 + 3 + 2 + 1 = 9 and 9 is divisible by 3.
• Divisibility By 4 : A number is divisible by 4 if the last two digits are divisible by 4. For example, 1234 is not divisible by 4 as the last two digits 34 is not divisible by 4. But, 1232 is divisible by 4 as the last two digits 32 is divisible by 4.
• Divisibility By 5 : A number is divisible by 5 if the last digit is either 0 or 5.
• Divisibility By 6 : A number is divisible by 6 if it is divisible by both 2 and 3. For example, 114 is divisible by 6 as it is divisible by both 2(last digit is 4) and 3 (1+1+4=6, 6 is divisible by 3).
• Divisibility By 7 : A number is divisible by 7 iff repeatedly doing following steps until a single digit left leaves the single digit as 0 or 7. (1) Remove the last digit. (2) Subtract double of last digit from the number obtained after step 1 (number with last digit removed). Example, given number is 196. After removing last digit, we get 19. After subtracting 12 (double of removed digit), we get 7. Since the last left digit is 7, number is multiple of 7.
• Divisibility By 8 : A number is divisible by 8 if the last three digits are divisible by 8. For example, 1234 is not divisible by 8 as the last three digits 234 is not divisible by 8. But, 1232 is divisible by 8 as the last three digits 232 is divisible by 8.
• Divisibility By 9 : A number is divisible by 9 if the sum of its digits is divisible by 9. For example, 12321 is divisible by 3 because 1 + 2 + 3 + 2 + 1 = 9 and 9 is divisible by 9.
• Divisibility By 11 : A number is divisible by 11 if the difference between the sum of numbers at even positions and odd positions is either 0 or a multiple of 11.

NOTE : If ‘p’ and ‘q’ are co-primes and we have a number ‘n’ that is divisible by both ‘p’ and ‘q’, ‘n’ will be divisible by p x q.
For example, 48 is divisible by both 3 and 8 and also by 3 x 8 = 24.
But, if ‘p’ and ‘q’ are NOT co-prime, then the fact that ‘n’ would be divisible by p x q given that ‘n’ is divisible by both ‘p’ and ‘q’ is not necessary. For example, 144 is divisible by both 8 and 12 (not co-prime), but it is not divisible by 8 x 12 = 96.
DIVISION THEOREM

• Dividend = (Divisor x Quotient) + Remainder
• (xn – an) is divisible by (x – a) for all values of n.
  For example, for n = 2, x2 – a2 = (x – a) (x + a), which is divisible by (x – a).
  Similarly, for n = 3, x3 – a3 = (x – a) (x2 + a2 + xa), which is divisible by (x – a).
• (xn – an) is divisible by (x + a) for all even values of n.
  For example, for n = 2, x2 – a2 = (x – a) (x + a), which is divisible by (x+a).
  Similarly, for n = 3, x3 – a3 = (x – a) (x2 + a2 + xa), which is not divisible by (x + a).
• (xn + an) is divisible by (x + a) for all odd values of n.
  For example, for n = 3, x3 + a3 = (x + a) (x2 + a2 – xa), which is divisible by (x + a).

• Sample Problems

  Question 1 : When a number is successively divided by 2, 3, 7, we get 1, 2, 3 as the remainder respectively. What is the smallest such number ?

  Solution : The number is of the form 2a+1, 3b+2, 7c+3. So, we put c=1 and proceed as follows :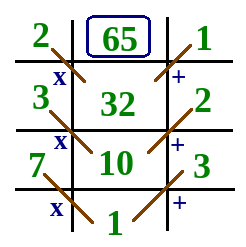

  
  

  Basically, we successively multiply the divisors with the result of the previous stage and add the corresponding remainder.

  7 x 1 + 3 = 10

  3 x 10 + 2 = 32

  2 x 32 + 1 = 65

  Thus, 65 is the required answer.

  NOTE : The answer would differ if we change the order of divisors. For smallest number, arrange the divisors in decreasing order.
  Question 2 : When a number is successively divided by 2, 4, 8, we get 1, 1, 0 as the remainder respectively. What is the smallest such number ?
  Solution : Proceeding in the similar manner as the above question,
  8 x 1 + 0 = 8
  4 x 8 + 1 = 33
  2 x 33 + 1 = 67
  Thus, 67 is the required answer.
  Question 3 : What would be the maximum value of ‘B’ in the following equation :

    1 2 B
  + B 4 C
  + C 6 7
  --------
    1035
  --------
  

  Solution : Only the leftmost part of the number can be of two or more digits. So, we split the answer as :

    1 2 B
  + B 4 C
  + C 6 7
  --------
   10 3 5
  --------
  

  Now, from column 1, we can easily infer that B + C = 8.
  First, let us consider B + C = 18. This is the case possible if and only if B = C = 9. So, the equation would be 129 + 949 + 967 = 2045, but we need 1035 as the answer. Thus, this is not the required case.
  So, B + C = 8. For maximum ‘B’, we put C = 0. Therefore, B = 8.
  Now, to verify our answer, we put B = 8 and C = 0 in the given equation.

    1 2 8
  + 8 4 0
  + 0 6 7
  --------
   10 3 5
  --------
  

  Therefore, our answer B = 8 is correct.
  Question 4 : Which of the following are prime numbers ?
  (i) 247
  (ii) 397
  (iii) 423
  Solution : 
  (i) 162 = 256 > 247. Prime numbers less than 16 are 2, 3, 5, 7, 11, 13 and 247 is divisible by 13. Therefore, 247 is not a prime number. It is a composite number.
  (ii) 202 = 400 > 397. Prime numbers less than 20 are 2, 3, 5, 7, 11, 13, 17, 19 but 397 is not divisible by any of these. Therefore, 397 is a prime number.
  (iii) 212 = 441 > 423. Prime numbers less than 21 are 2, 3, 5, 7, 11, 13, 17, 19 and 423 is divisible by 3. Therefore, 423 is not a prime number. It is a composite number.
  Question 5 : Find the unit’s digit in the product (17)153 x (31)62.
  Solution : The unit’s digit of the given equation would be the same as the unit’s digit of the equation 7153 x 162.
  Now, we need to find a pattern in the unit’s digit when we gradually increase the powers of 7. 71 gives 7, 72 gives 9, 73 gives 3, 74 gives 1. So, at the fourth power, we get the unit’s digit as 1. Therefore, to make our work easy, we need to write the original power (153) in multiples of 4 to the closest extent possible. We multiply this power (4) by a number such that we get nearest to 153. So, 4 x 38 = 152 and 7152 also has 1 in the unit’s place.
  Now, (17)153 has 7 at unit’s place and (31)62 has 1 at the unit’s place.
  Therefore, the problem simply reduces to 7 x 1 = 7.
  Hence, the unit’s digit is 7.
  Question 6 : Find the unit’s digit in (17)153 + (31)62.
  Solution : The unit’s digit of the given equation would be the same as the unit’s digit of the equation 7153 + 162.
  Now, we need to find a pattern in the unit’s digit when we gradually increase the powers of 7. 71 gives 7, 72 gives 9, 73 gives 3, 74 gives 1. So, at the fourth power, we get the unit’s digit as 1. Therefore, to make our work easy, we need to write the original power (153) in multiples of 4 to the closest extent possible. We multiply this power (4) by a number such that we get nearest to 153. So, 4 x 38 = 152 and 7152 also has 1 in the unit’s place.
  Now, (17)153 has 7 at unit’s place and (31)62 has 1 at the unit’s place.
  Therefore, the problem simply reduces to 7 + 1 = 8.
  Hence, the unit’s digit is 8.
  Question 7 : Find the total number of prime factors in the expression (14)11 x (7)2 x (11)3 .
  Solution : (14)11 x (7)2 x (11)3 = (2 x 7)11 x (7)2 x (11)3 = (2)11 x (7)11 x (7)2 x (11)3 = (2)11 x (7)13 x (11)3
  Therefore, total number of prime factors = 11 + 13 + 3 = 27
  Question 8 : Which digits should come in place of * and # such that the number 12386*# is divisible by both 8 and 5 ?
  Solution : Since the given number should be divisible by 5, 0 or 5 must come in place of #. But, a number ending with 5 is never divisible by 8. So, 0 will replace #.
  Now, the number formed by the last three digits is 6*0, which becomes divisible by 8, if * is replaced by 0 or 4 or 8.
  Hence, digits in place of * and # are 0 or 4 or 8 and 0 respectively.
  Question 9 : What is the least number that must be subtracted from 9999 to make it exactly divisible by 19 ?
  Solution : On dividing 9999 by 19, we get 5 as remainder. Therefore, number to be subtracted = 5.
  Question 10 : What is the least number that must be added to 9999 to make it exactly divisible by 19 ?
  Solution : On dividing 9999 by 19, we get 5 as remainder. Therefore, number to be added = 19 – 5 = 14.
  Question 11 : A number when divided by 340 gives a remainder 47. What would be the remainder when the same number is divided by 17 ?
  Solution : The number is of the form 340a + 47 = 17 * (20a) + 17 * (2) + 13 = 17 * (20a + 2) + 13.
  Therefore, on dividing this number by 17, we would get 13 as the remainder.
  Question 12 : Find the remainder when 321 is divided by 5.
  Solution : 34 = 81. So, the unit’s digit of 34 is 1.
  Therefore, the unit’s digit of 320 = 1 and thus, the unit’s digit of 321 = 1*3 = 3.
  3 when divided by 5 gives 3 as the remainder.
  So, the remainder when 321 is divided by 5 is 3.

 LCM and HCF

• Factors and Multiples : All the numbers that divide a number completely, i.e., without leaving any remainder, are called factors of that number. For example, 24 is completely divisible by 1, 2, 3, 4, 6, 8, 12, 24. Each of these numbers is called a factor of 24 and 24 is called a multiple of each of these numbers.
• LCM : The least number which is exactly divisible by each of the given numbers is called the least common multiple of those numbers. For example, consider the numbers 3, 31 and 62 (2 x 31). The LCM of these numbers would be 2 x 3 x 31 = 186.
  To find the LCM of the given numbers, we express each number as a product of prime numbers. The product highest power of the prime numbers that appear in prime factorization of any of the numbers gives us the LCM.
  For example, consider the numbers 2, 3, 4 (2 x 2), 5, 6 (2 x 3). The LCM of these numbers is 2 x 2 x 3 x 5 = 60. The highest power of 2 comes from prime factorization of 4, the highest power of 3 comes from prime factorization of 3 and prime factorization of 6 and the highest power of 5 comes from prime factorization of 5.
• HCF : The largest number that divides two or more numbers is the highest common factor (HCF) for those numbers. For example, consider the numbers 30 (2 x 3 x 5), 36 (2 x 2 x 3 x 3), 42 (2 x 3 x 7), 45 (3 x 3 x 5). 3 is the largest number that divides each of these numbers, and hence, is the HCF for these numbers.
  HCF is also known as Greatest Common Divisor (GCD).
  
  To find the HCF of two or more numbers, express each number as product of prime numbers. The product of the least powers of common prime terms gives us the HCF. This is the method we illustrated in the above step.
  Also, for finding the HCF of two numbers, we can also proceed by long division method. We divide the larger number by the smaller number (divisor). Now, we divide the divisor by the remainder obtained in the previous stage. We repeat the same procedure until we get zero as the remainder. At that stage, the last divisor would be the required HCF.
  For example, we find the HCF of 30 and 42.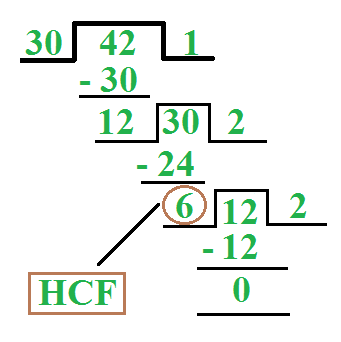
  
• For two numbers ‘a’ and ‘b’, LCM x HCF = a x b
• HCF of co-primes = 1
• For two fractions,
  HCF = HCF (Numerators) / LCM (Denominators)
  LCM = LCM (Numerators) / HCF (Denominators)

Sample Problems

Question 1 : Two numbers are in the ratio of 5:11. If their HCF is 7, find the numbers.
Solution : Let the numbers be 5m and 11m. Since 5:11 is already the reduced ratio, ‘m’ has to be the HCF. So, the numbers are 5 x 7 = 35 and 11 x 7 = 77.

Question 2 : Find the length of the plank which can be used to measure exactly the lengths 4 m 50 cm, 9 m 90 cm and 16 m 20 cm in the least time.
Solution : Let us first convert each length to cm. So, the lengths are 450 cm, 990 cm and 1620 cm. Now, we need to find the length of the largest plank that can be used to measure these lengths as the largest plank will take the least time. For this, we need to take the HCF of 450, 990 and 1620.
450 = 2 x 3 x 3 x 5 x 5 = 2 x 32 x 52
990 = 2 x 3 x 3 x 5 x 11 = 2 x 32 x 5 x 11
1620 = 2 x 2 x 3 x 3 x 3 x 3 x 5 = 22 x 34 x 5
Therefore, HCF (450, 990, 1620) = 2 x 3 x 3 x 5 = 90
Thus, we need a plank of length 90 cm to measure the given lengths in the least time.

Question 3 : Find the greatest number which on dividing 70 and 50 leaves remainders 1 and 4 respectively.
Solution : The required number leaves remainders 1 and 4 on dividing 70 and 50 respectively. This means that the number exactly divides 69 and 46.
So, we need to find the HCF of 69 (3 x 23) and 46 (2 x 23).
HCF (69, 46) = 23
Thus, 23 is the required number.

Question 4 : Find the largest number which divides 64, 136 and 238 to leave the same remainder in each case.
Solution : To find the required number, we need to find the HCF of (136-64), (238-136) and (238-64), i.e., HCF (72, 102, 174).
72 = 23 x 32
102 = 2 x 3 x 17
174 = 2 x 3 x 29
Therefore, HCF (72, 102, 174) = 2 x 3 = 6
hence, 6 is the required number.

Question 5 : Find the least number which when divided by 5,7,9 and 12, leaves the same remainder 3 in each case
Solution : In these type of questions, we need to find the LCM of the divisors and add the common remainder (3) to it.
So, LCM (5, 7, 9, 12) = 1260
Therefore, required number = 1260 + 3 = 1263

Question 6 : Find the largest four digit number exactly divisible by 15,21 and 28.
Solution : The largest four digit number is 9999.
Now, LCM (15, 21, 28) = 420
On dividing 9999 by 420, we get 339 as the remainder.
Therefore, the required number is 9999-339 = 9660

Question 7 : The policemen at three different places on a ground blow a whistle after every 42 sec, 60 sec and 78 sec respectively. If they all blow the whistle simultaneously at 9:30:00 hours, then at what time do they whistle again together ?
Solution : They all will whistle again at the same time after an interval that is equal to the LCM of their individual whistle blowing cycles.
So, LCM (42, 60, 78) = 2 x 3 x 7 x 10 x 13 = 5460
Therefore, they will blow the whistle again simultaneously after 5460 sec, i.e., after 1 hour 31 minutes, i.e., at 11:01:00 hours.

Question 8 : Find the least number which when divided by 6,7,8 leaves a remainder 3, but when divided by 9 leaves no remainder .
Solution : LCM (6, 7, 8) = 168
So, the number is of the form 168m + 3.
Now, 168m + 3 should be divisible by 9.
We know that a number is divisible by 9 if the sum of its digits is a multiple of 9.
For m = 1, the number is 168 + 3 = 171, the sum of whose digits is 9.
Therefore, the required number is 171.

Question 9 : Two numbers are in the ratio 2:3. If the product of their LCM and HCF is 294, find the numbers.
Solution : Let the common ratio be ‘m’. So, the numbers are 2m and 3m.
Now, we know that Product of numbers = Product of LCM and HCF.
=> 2m x 3m = 294
=> m2 = 49
=> m = 7
Therefore, the numbers are 14 and 21.

Question 10 : A rectangular field of dimension 180m x 105m is to be paved by identical square tiles. Find the size of each tile and the number of tiles required.
Solution : We need to find the size of a square tile such that a number of tiles cover the field exactly, leaving no area unpaved.
For this, we find the HCF of the length and breadth of the field.
HCF (180, 105) = 15
Therefore, size of each tile = 15m x 15m
Also, number of tiles = area of field / area of each tile
=> Number of tiles = (180 x 105) / (15 x 15)
=> Number of tiles = 84
Hence, we need 84 tiles, each of size 15m x 15m.

Question 11 : Three rectangular fields having area 60 m2, 84 m2 and 108 m2 are to be divided into identical rectangular flower beds, each having length 6 m. Find the breadth of each flower bed.
Solution : We need to divide each large field into smaller flower beds such that the area of each bed is same.
So, we find the HCF of the larger fields that gives us the area of the smaller field.
HCF (60, 84, 108) = 12
Now, this HCF is the area (in m2) of each flower bed.
Also, area of a rectangular field = Length x Breadth
=> 12 = 6 x Breadth
=> Breadth = 2 m
Hence, each flower bed would be 2 m wide.

Question 12 : Find the maximum number of students among whom 182 chocolates and 247 candies can be distributed such that each student gets same number of each. Also, find the number of chocolates and candies each student will get.
Solution : We need to find the HCF of the number of chocolates and candies available, which would give us the number of students.
HCF (182, 247) = 13
So, there can be 13 students.
Also, Number of chocolates for each student = 182 / 13 = 14
Number of toffees for each student = 247 / 13 = 19